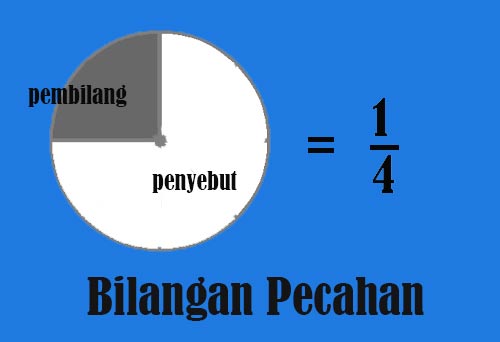
Pengertian Pecahan Dalam Matematika

Yang dimaksud dengan pecahan dalam matematika adalah bilangan rasional yang dapat ditulis dalam bentuk a/b (dibaca a per b), dengan bentuk dimana a dan b merupakan bilangan bulat, b tidak sama dengan nol, dan bilangan a bukan kelipatan bilangan b. Secara sederhana, dapat dikatakan pecahan merupakan sebuah bilangan yang memiliki pembilang dan penyebut.

Untuk menjelaskan pengertian bilangan pecahan sebagai bagian dari sesuatu yang utuh dapat menggunakan gambar ilustrasi, dimana bagian yang dimaksud adalah bagian yang diperhatikan (ditandai dengan arsiran). Bagian yang diarsir dinamakan pembilang dan yang utuh dianggap sebagai satuan dan dinamakan penyebut.

Penjumlahan Pecahan

Dalam pecahan terdapat operasi penjumlahan pecahan.Operasi penjumlahan pecahan dibedakan menjadi dua macam, yaitu penjumlahan pecahan yang berpenyebut sama dan penjumlahan pecahan yang berpenyebut beda,

1. Penjumlahan pecahan berpenyebut sama

Penjumlahan pecahan berpenyebut sama supaya dapat diperoleh hasilnya dengan menjumlahkan pembilangnya, sedangkan penyebutnya tetap,

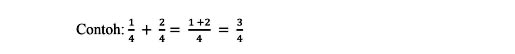
2. Penjumlahan pecahan berpenyebut berbeda

Penjumlahan pecahan berpenyebut berbeda supaya dapat memperoleh hasilnya maka penyebutnya harus disamakan terlebih dahulu yaitu dengan mencari pecahan senilai atau mencari KPK (Kelipatan Persekutuan terKecil) dari kedua penyebut.

a) Penjumlahan pecahan berpenyebut berbeda dengan mencari pecahan senilai.

b) Penjumlahan pecahan berpenyebut berbeda dengan mencari KPK (Kelipatan Persekutuan terKecil).

Pengurangan Pecahan

Pada dasarnya pengurangan pada pecahan sama saja dengan konsep penjumlahan. Akan tetapi, pengurangan bisa dilakukan langsung apabila penyebutnya sama dan apabila penyebut dari kedua pecahan yang dikurangkan adalah tidak sama (berbeda) maka harus disamakan terlebih dahulu.

Contoh:

Penyebut sama: